| diagram |  |
||||||||||||||||||||||||||||||
| namespace | http://www.opengis.net/gml | ||||||||||||||||||||||||||||||
| type | extension of gml:AbstractCurveSegmentType | ||||||||||||||||||||||||||||||
| properties |
|
||||||||||||||||||||||||||||||
| children | gml:refLocation gml:scaleFactor gml:startParameter gml:endParameter | ||||||||||||||||||||||||||||||
| used by |
|
||||||||||||||||||||||||||||||
| attributes |
|
||||||||||||||||||||||||||||||
| annotation |
|
||||||||||||||||||||||||||||||
| source | <xs:complexType name="ClothoidType"> <xs:annotation> <xs:documentation>A clothoid, or Cornu's spiral, is plane curve whose curvature is a fixed function of its length. In suitably chosen co-ordinates it is given by Fresnel's integrals. x(t) = 0-integral-t cos(AT*T/2)dT y(t) = 0-integral-t sin(AT*T/2)dT This geometry is mainly used as a transition curve between curves of type straight line to circular arc or circular arc to circular arc. With this curve type it is possible to achieve a C2-continous transition between the above mentioned curve types. One formula for the Clothoid is A*A = R*t where A is constant, R is the varying radius of curvature along the the curve and t is the length along and given in the Fresnel integrals.</xs:documentation> </xs:annotation> <xs:complexContent> <xs:extension base="gml:AbstractCurveSegmentType"> <xs:sequence> <xs:element name="refLocation"> <xs:complexType> <xs:sequence> <xs:element ref="gml:AffinePlacement"> <xs:annotation> <xs:documentation>The "refLocation" is an affine mapping that places the curve defined by the Fresnel Integrals into the co-ordinate reference system of this object.</xs:documentation> </xs:annotation> </xs:element> </xs:sequence> </xs:complexType> </xs:element> <xs:element name="scaleFactor" type="decimal"> <xs:annotation> <xs:documentation>The element gives the value for the constant in the Fresnel's integrals.</xs:documentation> </xs:annotation> </xs:element> <xs:element name="startParameter" type="double"> <xs:annotation> <xs:documentation>The startParameter is the arc length distance from the inflection point that will be the start point for this curve segment. This shall be lower limit used in the Fresnel integral and is the value of the constructive parameter of this curve segment at its start point. The startParameter can either be positive or negative. NOTE! If 0.0 (zero), lies between the startParameter and the endParameter of the clothoid, then the curve goes through the clothoid's inflection point, and the direction of its radius of curvature, given by the second derivative vector, changes sides with respect to the tangent vector. The term length distance for the</xs:documentation> </xs:annotation> </xs:element> <xs:element name="endParameter" type="double"> <xs:annotation> <xs:documentation>The endParameter is the arc length distance from the inflection point that will be the end point for this curve segment. This shall be upper limit used in the Fresnel integral and is the value of the constructive parameter of this curve segment at its start point. The startParameter can either be positive or negative.</xs:documentation> </xs:annotation> </xs:element> </xs:sequence> </xs:extension> </xs:complexContent> </xs:complexType> |
element ClothoidType/refLocation
| diagram | 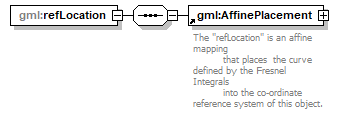 |
||||
| namespace | http://www.opengis.net/gml | ||||
| properties |
|
||||
| children | gml:AffinePlacement | ||||
| source | <xs:element name="refLocation"> <xs:complexType> <xs:sequence> <xs:element ref="gml:AffinePlacement"> <xs:annotation> <xs:documentation>The "refLocation" is an affine mapping that places the curve defined by the Fresnel Integrals into the co-ordinate reference system of this object.</xs:documentation> </xs:annotation> </xs:element> </xs:sequence> </xs:complexType> </xs:element> |
element ClothoidType/scaleFactor
| diagram |  |
||||
| namespace | http://www.opengis.net/gml | ||||
| type | xs:decimal | ||||
| properties |
|
||||
| annotation |
|
||||
| source | <xs:element name="scaleFactor" type="decimal"> <xs:annotation> <xs:documentation>The element gives the value for the constant in the Fresnel's integrals.</xs:documentation> </xs:annotation> </xs:element> |
element ClothoidType/startParameter
| diagram |  |
||||
| namespace | http://www.opengis.net/gml | ||||
| type | xs:double | ||||
| properties |
|
||||
| annotation |
|
||||
| source | <xs:element name="startParameter" type="double"> <xs:annotation> <xs:documentation>The startParameter is the arc length distance from the inflection point that will be the start point for this curve segment. This shall be lower limit used in the Fresnel integral and is the value of the constructive parameter of this curve segment at its start point. The startParameter can either be positive or negative. NOTE! If 0.0 (zero), lies between the startParameter and the endParameter of the clothoid, then the curve goes through the clothoid's inflection point, and the direction of its radius of curvature, given by the second derivative vector, changes sides with respect to the tangent vector. The term length distance for the</xs:documentation> </xs:annotation> </xs:element> |
element ClothoidType/endParameter
| diagram |  |
||||
| namespace | http://www.opengis.net/gml | ||||
| type | xs:double | ||||
| properties |
|
||||
| annotation |
|
||||
| source | <xs:element name="endParameter" type="double"> <xs:annotation> <xs:documentation>The endParameter is the arc length distance from the inflection point that will be the end point for this curve segment. This shall be upper limit used in the Fresnel integral and is the value of the constructive parameter of this curve segment at its start point. The startParameter can either be positive or negative.</xs:documentation> </xs:annotation> </xs:element> |
XML Schema documentation generated by XMLSpy Schema Editor http://www.altova.com/xmlspy